环形链表的起点

a view of a mountain range with clouds in the sky

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

img

1
2
3
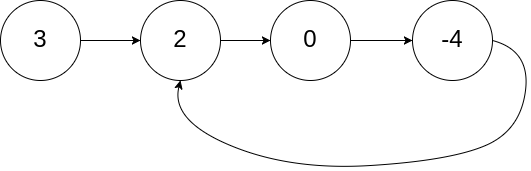
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

img

1
2
3
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public ListNode detectCycle(ListNode head) {
         ListNode fast = head;
       ListNode slow = head;
       while (fast != null && fast.next != null) {
           fast = fast.next.next;
           slow = slow.next;
           if (fast == slow){
               break;
           }
       }
       // fast 遇到空指针说明没有环
       if (fast == null || fast.next == null){
           return null;
       }
       // 将慢指针指向head节点，重新开始单步走，当相交的时候，就是环的起点。
       slow = head;
       while (slow != fast) {
           fast = fast.next;
           slow = slow.next;
       }
       return slow;
   }

我们假设快慢指针相遇时，慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步：

img

fast 一定比 slow 多走了 k 步，这多走的 k 步其实就是 fast 指针在环里转圈圈，所以 k 的值就是环长度的「整数倍」。

假设相遇点距环的起点的距离为 m，那么结合上图的 slow 指针，环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。

巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。因为结合上图的 fast 指针，从相遇点开始走k步可以转回到相遇点，那走 k - m 步肯定就走到环起点了：

img

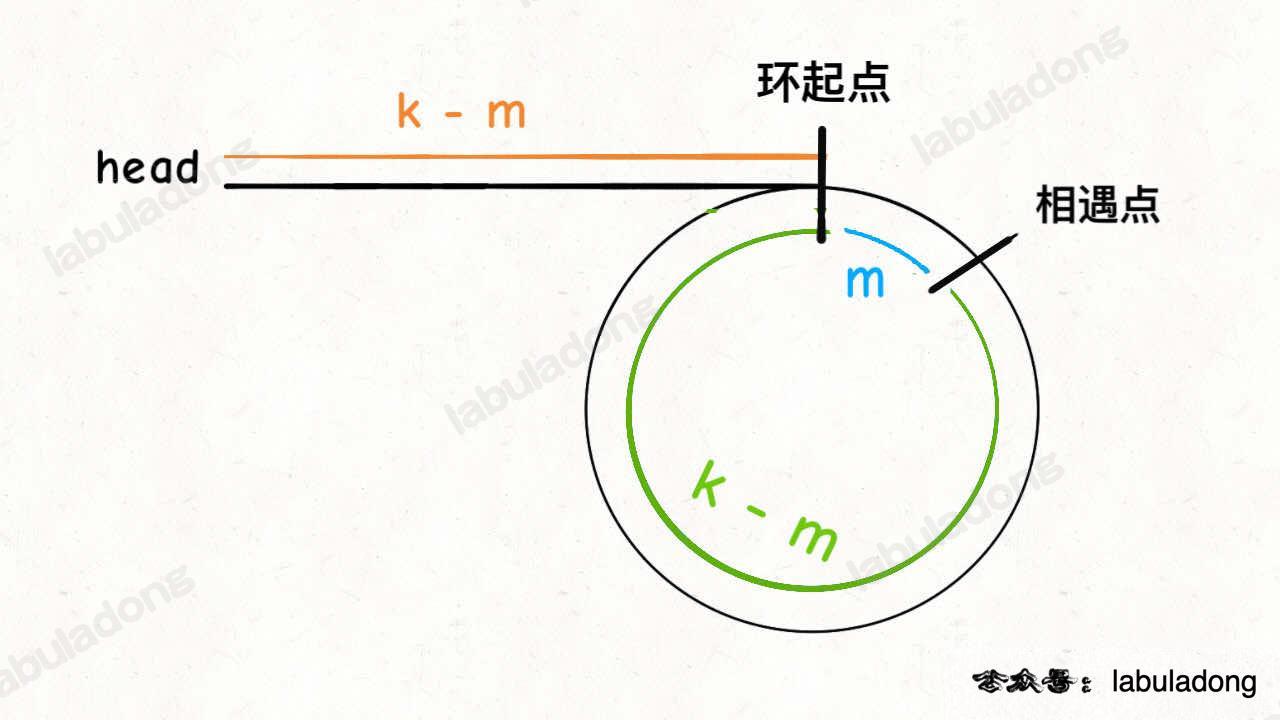
所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了